how to find terminal point

TERMINAL POINTS ON THE UNIT CIRCLE

Suppose t is a real number. Let's mark off a distance t along the unit circle, starting at the point (1, 0) and moving in a counterclockwise direction, if t is positive or in a clockwise direction, if t is negative.

In this way we arrive at a point P(x, y) on the unit circle. The point P(x, y) obtained in this way is called the terminal point determined by the real number t.

Terminal Point P(x, y) Determined by t > 0 :

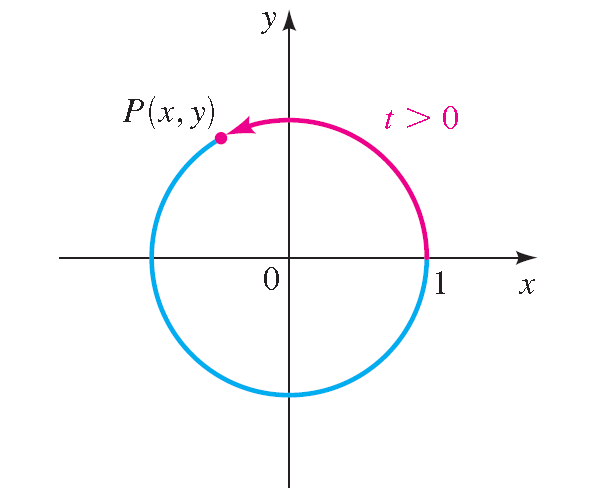
Terminal Point P(x, y) Determined by t < 0 :

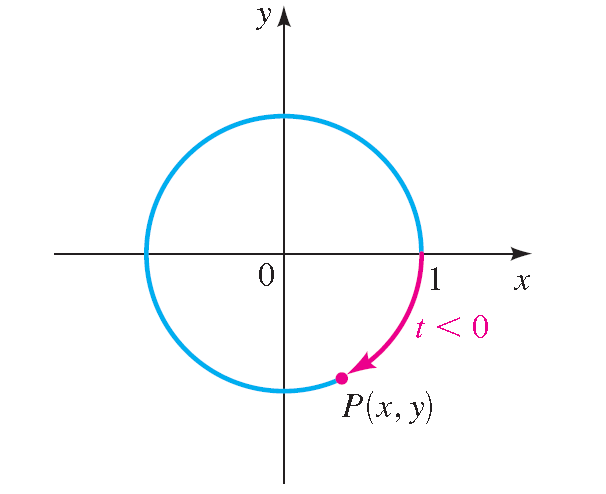
The circumference of the unit circle is

C = 2π(1) = 2 π

So, if a point starts at (1, 0) and moves counterclockwise all the way around the unit circle and returns to (1, 0), it travels a distance of 2π. To move halfway around the circle, it travels a distance of (1/2)(2π) = π.

To move a quarter of the distance around the circle, it travels a distance of (1/4)(2π) = π/2. Where does the point end up when it travels these distances along the circle? In the diagram shown below, we see, for example, that when it travels a distance ofπ starting at (1, 0), its terminal point is (-1, 0).

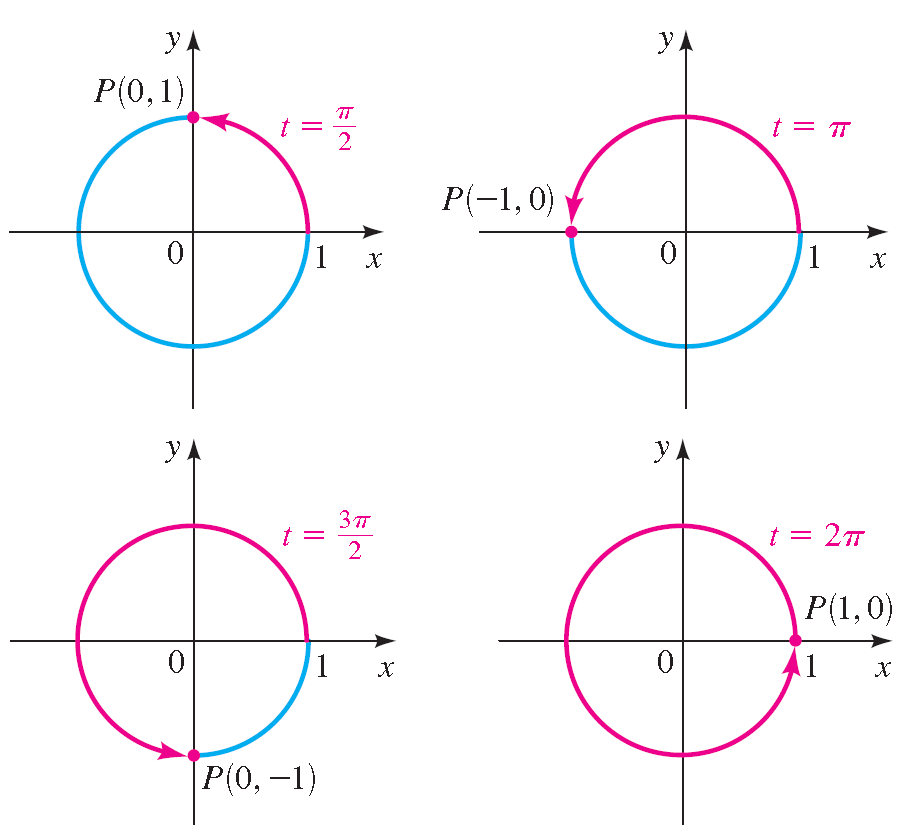
Finding Terminal Points

Find the terminal point on the unit circle determined by each real number t.

Example 1 :

t = 3π

Solution :

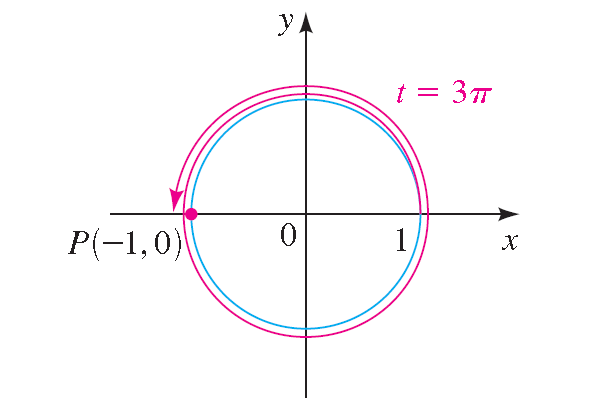
The terminal point determined by 3π is (-1, -0).

Example 2 :

t = -π

Solution :

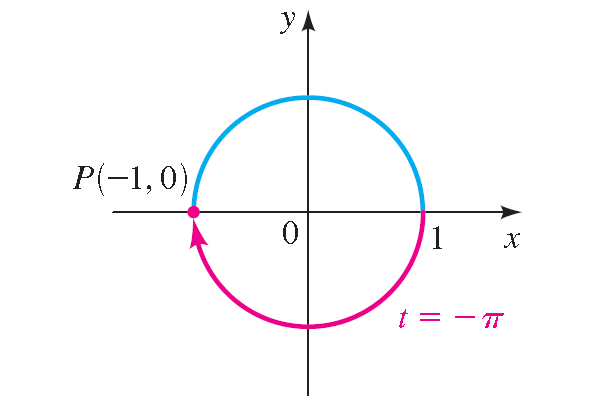
The terminal point determined by -π is (-1, -0).

Example 3 :

t = -π/2

Solution :

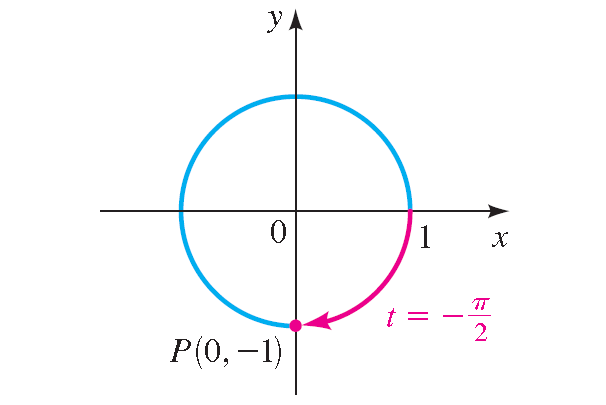
The terminal point determined by -π/2 is (0, -1).

Notice that different values of t can determine the same terminal point.

The terminal point P(x, y) determined by t =π/4 is the same distance from (1, 0) as from (0, 1) along the unit circle.

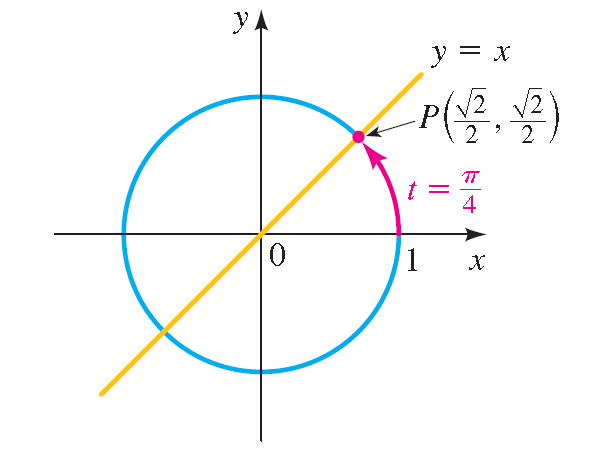
Since the unit circle is symmetric with respect to the line y = x, it follows that P lies on the line y = x. So P is the point of intersection (in the first quadrant) of the circlex ² + y ² = 1 and the line y = x.

Substituting x for y in the equation of the unit circle.

x ² + x ² = 1

2x² = 1

x² = 1/2

k = ± 1/√2

Because P is in the first quadrant, x = 1/√2 and y = x, we have y = 1/ √ 2 also.

Thus the terminal point determined by π/4 is

P(1/ √ 2, 1/ √ 2) = P( √ 2/2, √ 2/2)

Similar methods can be used to find the terminal points determined by t = π/6 and t = π/3.

Table :

π/6

π/4

π/3

π/2

Terminal point determined by t

(1, 0)

(√3/2, 1/2)

(√2/2, √2/2)

(1/2, √3/2)

(0, 1)

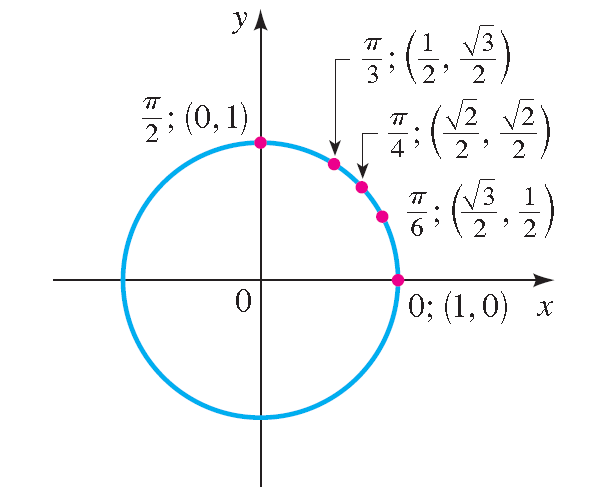
Example 4 :

t = -π/4

Solution :

Let P be the terminal point determined by - π/4, and let Q be the terminal point determined by π/4. In the diagram shown below, we see that the point P has the same coordinates as Q except for sign.

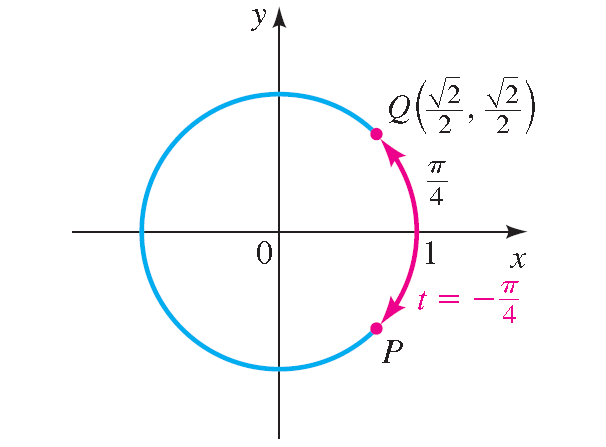
Because P is in quadrant IV, its x-coordinate is positive and its y-coordinate is negative. Thus, the terminal point is

P( √2/2, - √2/2)

Example 5 :

t = 3π/4

Solution :

Let P be the terminal point determined by 3 π/4, and let Q be the terminal point determined by π/4. In the diagram shown below, we see that the point P has the same coordinates as Q except for sign.

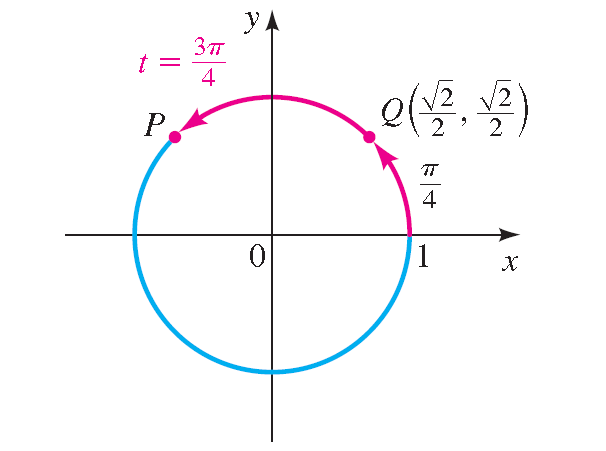
BecauseP is in quadrant II, its x-coordinate is negative and its y-coordinate is positive. Thus, the terminal point is

P(-√2/2, √2/2)

Example 6 :

t = -5π/6

Solution :

Let P be the terminal point determined by -5 π/6, and let Q be the terminal point determined by π/6. In the diagram shown below, we see that the point P has the same coordinates as Q except for sign.

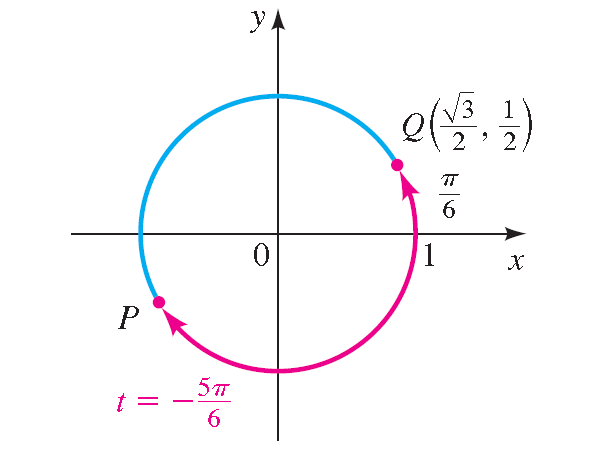
Because P is in quadrant III, its both x-coordinate and y-coordinate are negative. Thus, the terminal point is

P(- √3/2, -1 /2)

Related Stuff

1. The Unit Circle

2. Reference Number on the Unit Circle

3. Using Reference Number to Find terminal Points

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

If you have any feedback about our math content, please mail us :

v4formath@gmail.com

We always appreciate your feedback.

You can also visit the following web pages on different stuff in math.

WORD PROBLEMS

HCF and LCM word problems

Word problems on simple equations

Word problems on linear equations

Word problems on quadratic equations

Algebra word problems

Word problems on trains

Area and perimeter word problems

Word problems on direct variation and inverse variation

Word problems on unit price

Word problems on unit rate

Word problems on comparing rates

Converting customary units word problems

Converting metric units word problems

Word problems on simple interest

Word problems on compound interest

Word problems on types of angles

Complementary and supplementary angles word problems

Double facts word problems

Trigonometry word problems

Percentage word problems

Profit and loss word problems

Markup and markdown word problems

Decimal word problems

Word problems on fractions

Word problems on mixed fractrions

One step equation word problems

Linear inequalities word problems

Ratio and proportion word problems

Time and work word problems

Word problems on sets and venn diagrams

Word problems on ages

Pythagorean theorem word problems

Percent of a number word problems

Word problems on constant speed

Word problems on average speed

Word problems on sum of the angles of a triangle is 180 degree

OTHER TOPICS

Profit and loss shortcuts

Percentage shortcuts

Times table shortcuts

Time, speed and distance shortcuts

Ratio and proportion shortcuts

Domain and range of rational functions

Domain and range of rational functions with holes

Graphing rational functions

Graphing rational functions with holes

Converting repeating decimals in to fractions

Decimal representation of rational numbers

Finding square root using long division

L.C.M method to solve time and work problems

Translating the word problems in to algebraic expressions

Remainder when 2 power 256 is divided by 17

Remainder when 17 power 23 is divided by 16

Sum of all three digit numbers divisible by 6

Sum of all three digit numbers divisible by 7

Sum of all three digit numbers divisible by 8

Sum of all three digit numbers formed using 1, 3, 4

Sum of all three four digit numbers formed with non zero digits

Sum of all three four digit numbers formed using 0, 1, 2, 3

Sum of all three four digit numbers formed using 1, 2, 5, 6